সমকোন তৈরীকরণ আজেকর ক্লাসের বিষয়। সমকোন তৈরীকরণ ক্লাসটি কন্সট্রাকশন প্রসেসকোর্সের অংশ। কন্সট্রাকশন প্রসেস কোর্সটি বাংলাদেশ কারিগরি শিক্ষা বোর্ডের, ডিপ্লোমা ইন ইঞ্জিনিয়ারিং ডিসিপ্লিনের, ডিপ্লোমা ইন সিভিল ইঞ্জিনিয়ারিং টেকনোলোজির অংশ।
Table of Contents
সমকোন তৈরীকরণ
সমকোণ
যে কোণের পরিমাপ ৯০° তাকে সমকোণ বলে। অতএব, ৯০° পরিমাপের কোণই হলো সমকোণ। এভাবে ডিগ্রির সাহায্যে সমকোণকে সংজ্ঞায়িত করা যায়। তবে সমকোণকে এভাবে সংজ্ঞায়িত করার জন্য ডিগ্রি সম্বন্ধে পূর্বজ্ঞান থাকা আবশ্যক। তাহলে ডিগি কি – তা একটু জেনে নেওয়া যাক। পরস্পর লম্বভাবে পতিত দুইটি রশ্মির প্রান্তবিন্দু একই হলে রশ্মি দুইটি তাদের সাধারণ প্রান্তবিন্দুতে যে কোণে আনত, তার পরিমাপ ৯০°। এই কোণকে সমানভাবে ৯০ ভাগে ভাগ করলে প্রতি ভাগের পরিমাপ এক ডিগি বা ১° বিবেচনা করা হয়।
অন্যভাবে বললে, একটি রশ্মির প্রান্তবিন্দু একটি সরলরেখার উপর স্থাপন করলে উৎপন্ন সন্নিহিত কোণ দুইটির পরিমাপ সমান হলে কোণ দুইটির প্রত্যেকটিকে সমকোণ বলে। সমকোণের এই সংজ্ঞার সাথে ইউক্লিড প্রদত্ত সংজ্ঞার হুবহু মিল খুঁজে পাওয়া যায়।
তাছাড়া সমকোণ কেবল দুইটি রেখাংশ, রশ্মি বা সরলরেখা দ্বারাই তৈরি হতে পারে – তা কিন্তু নয়। দুইটি তল দ্বারাও সমকোণ গঠিত হতে পারে। দুইটি সমতল পরস্পর লম্বভাবে মিলিত হলেও সমকোণ তৈরি হয়।
তাহলে চুড়ান্তভাবে সমকোণকে সংজ্ঞায়িত করলে দাঁড়ায়, পরস্পর লম্বভাবে পতিত দুইটি রশ্মির প্রান্তবিন্দু একই হলে রশ্মি দুইটির প্রান্তবিন্দুতে উৎপন্ন কোণকে সমকোণ বলে। সুতরাং ১ সমকোণ = ৯০°। সমতল জ্যামিতি সমকোণ নিয়ে আলোচনা করে।
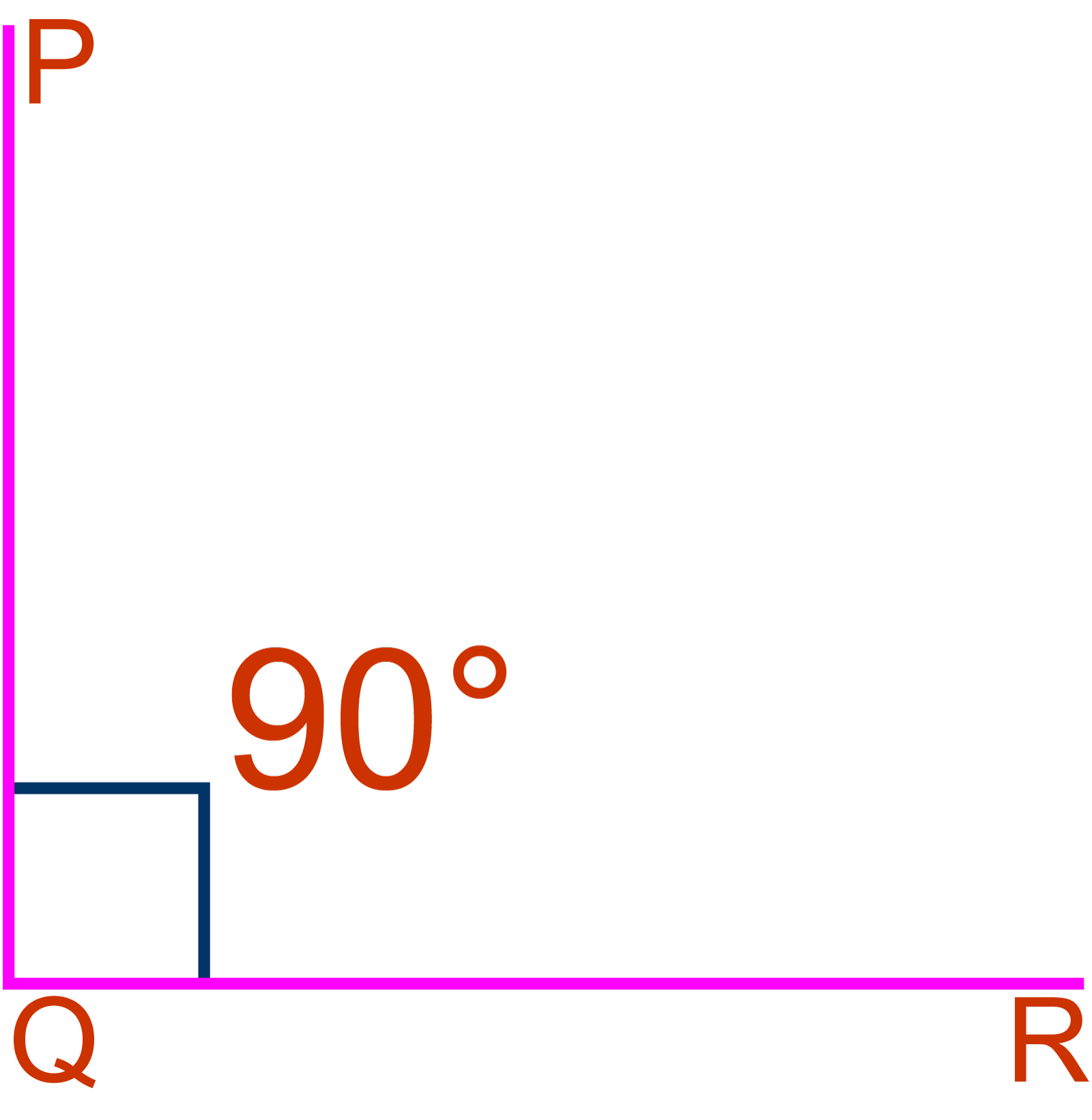
সমকোণের বিভিন্ন রূপ
সমকোণকে ভিন্ন ভিন্ন এককের মাধ্যমে ভিন্ন ভিন্ন রূপে প্রকাশ করা যায়।
- এক-চতুর্থাংশ চক্র
- ৯০° (ডিগ্রি)
- π2 রেডিয়ান
- ১০০ গ্রেডিয়ান
এক-চতুর্থাংশ চক্র
এক-চতুর্থাংশ চক্র বলতে বুঝায়, একটি বৃত্তের চারদিকে এক চক্রের চার ভাগের এক ভাগ। একটি রশ্মির প্রান্তবিন্দুকে একটি বৃত্তের কেন্দ্রে স্থির রেখে রশ্মিটিকে বৃত্তের চার ভাগের এক ভাগ ঘুরালে যে কোণ উৎপন্ন হয় তার পরিমাপ এক সমকোণ। এক চক্রে বৃত্তের কেন্দ্রে ৩৬০° কোণ উৎপন্ন হয়।
∴ ৩৬০° = ১ চক্র
বা, ৪ × ৯০° = ১ চক্র
বা, ৯০° = ১৪ চক্র
∴ ১ সমকোণ = এক-চতুর্থাংশ চক্র
সমকোণের বৈশিষ্ট্য
সমকোণকে বিশ্লেষণ করলে যেসব সমকোণের বৈশিষ্ট্য সমূহ পাওয়া যায় সেগুলো নিম্নরূপঃ
- সমকোণের পরিমাপ ৯০°।
- একটি সমকোণকে যেকোনো অনুপাতে দ্বিখণ্ডিত করলে যে দুইটি কোণ উৎপন্ন হয় তারা পরস্পর পূরক কোণ।
- সমকোণের বাহু দুইটি পরস্পর লম্ব।
- রেডিয়ান কোণ হলো ২π সমকোণের সমান। অর্থাৎ, ১ রেডিয়ান = ২π সমকোণ।
- একটি ত্রিভুজের একটি কোণ সমকোণ হলে অপর দুইটি কোণের যোগফলও এক সমকোণ হয়।
- এক সমকোণ অপেক্ষা ছোট কোণকে সূক্ষ্মকোণ বলে।
- এক সমকোণের পরিমাপ একটি পূর্ণ চক্রের এক-চতুর্থাংশ।
- কোনো বৃত্তস্থ কোণ সমকোণ হলে উক্ত বৃত্তস্থ কোণটি হয় অর্ধ-বৃত্তস্থ কোণ।
- এক সমকোণকে সমান ৯০ ভাগে ভাগ করলে প্রতি ভাগকে ১° বলা হয়।
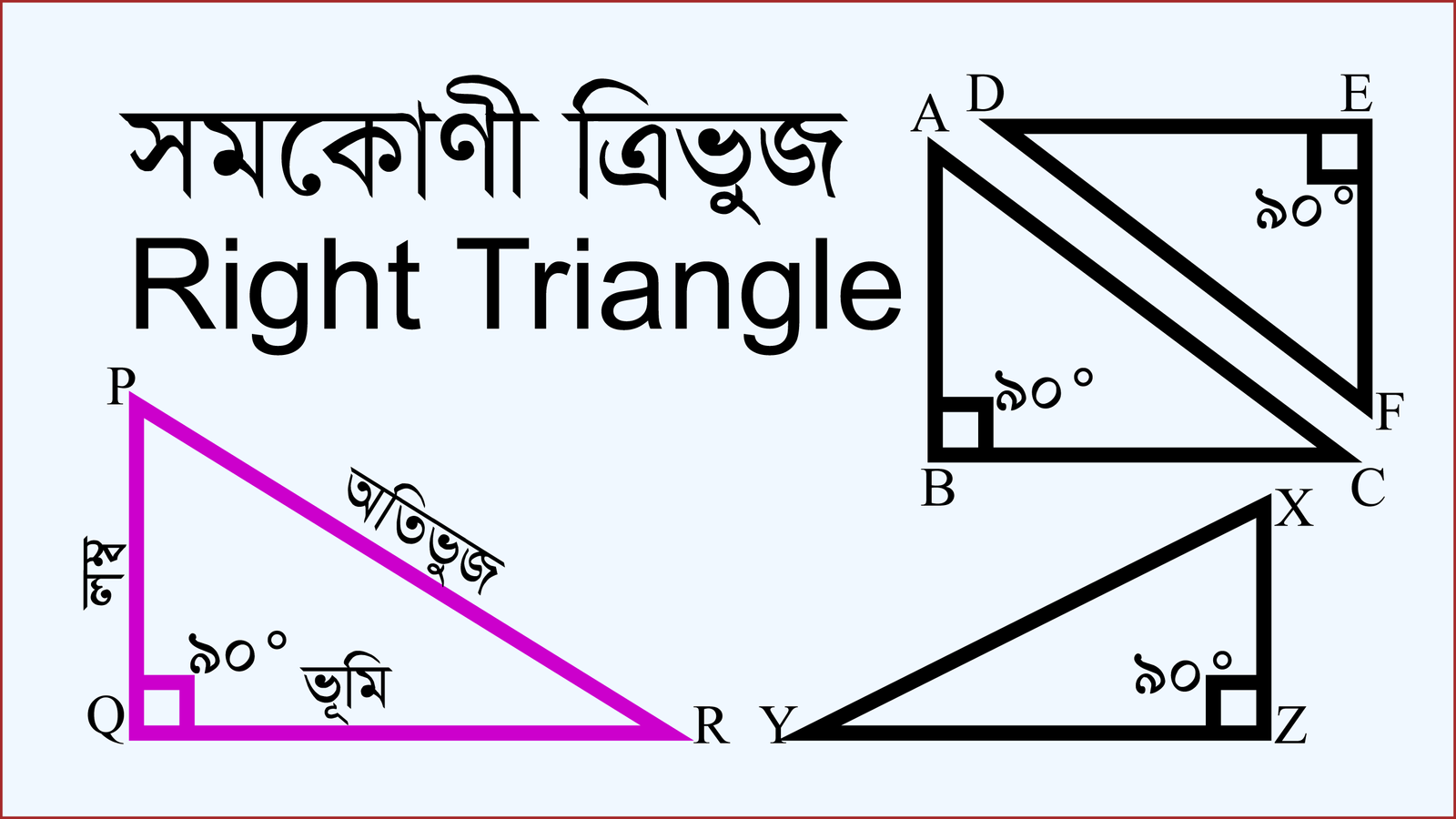
- সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভূজ বলে।
- একটি ত্রিভুজের একটি কোণ সমকোণ হলে অপর দুইটি কোণ পরস্পর পূরক কোণ।
- এক সমকোণের পরিমাপ ১০০ গ্রেডিয়ানের সমান। অর্থাৎ, ১ সমকোণ = ১০০ গ্রেডিয়ান।
- এক সমকোণ অপেক্ষা বড় এবং দুই সমকোণ অপেক্ষা ছোট কোণকে স্থূলকোণ বলে।
- চার সমকোণ মিলে একটি পূর্ণ কোণ তৈরি হয়।
- এক সমকোণের পরিমাপ π২ রেডিয়ানের সমান। অর্থাৎ, ১ সমকোণ = π২ রেডিয়ান।
- একটি সমকোণকে যেকোনো অনুপাতে ভাগ করলে যে দুইটি কোণ উৎপন্ন সেই কোণ দুইটি নিয়ে কোন ত্রিভুজ অঙ্কন করলে ত্রিভুজটি সমকোণী ত্রিভুজ হয়।
- সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুই বৃহত্তম বাহু।
- ইউক্লিড সমকোণের সাহায্যে লম্বরেখা, সূক্ষ্মকোণ এবং স্থূলকোণ বর্ণনা করেন।
