বলের সূত্র সম্পর্কে ধারণা | Structural Mechanics [ 66441 ]

বলের সূত্র সম্পর্কে ধারণা আজেকর ক্লাসের বিষয়। Understand the concept of laws of forces ক্লাসটি Structural Mechanics (66441) কোর্সের ২ অধ্যায়ের পাঠ। Structural Mechanics (66441) কোর্সটি বাংলাদেশ কারিগরি শিক্ষা বোর্ডের, পলিটেকনিক ডিসিপ্লিনের অংশ।

বলের সূত্র সম্পর্কে ধারণা

বর্ণনা (statement): কোনো বিন্দুতে ভিন্ন ভিন্ন রেখা বরাবর ক্রিয়ারত তিনটি বল সাম্যাবস্থায় থাকলে তাদের মান ও দিক একইক্রমে গৃহীত কোনো ত্রিভুজের তিনটি বাহু দ্বারা সূচিত করা যাবে।

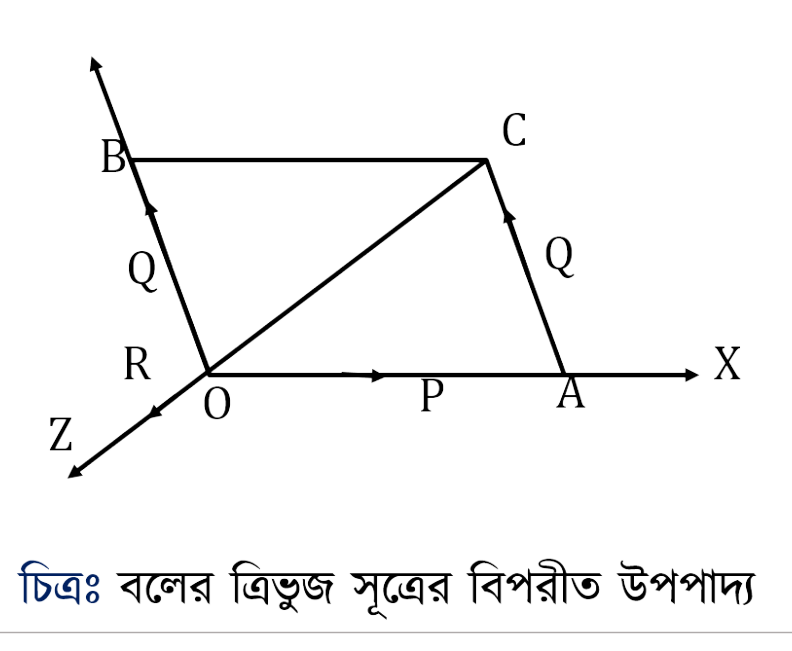
প্রমাণ (Proof): মনে করি, O বিন্দুতে OX, OY, OZ বরাবর ক্রিয়ারত তিনটি বল P, Q ও R সাম্যাবস্থায় আছে।

OX ও OY থেকে কোনো নির্দিষ্ট এককের পরিমাপে যথাক্রমে OA এবং OB অংশ কটে নিই যেন উহারা P ও Q বলদ্বয়কে (মানে ও দিকে) সূচিত করে। OACB সামান্তরিকটি অঙ্কন করে CO যোগ করি।

যেহেতু P, Q ও R বল তিনটি সাম্যাবস্থা সৃষ্টি করে, সুতরাং R বলটি P ও Q এর লব্ধির সমান ও বিপরীতমুখী হবে।

অর্থাৎ R বলটি মানে ও দিকে CO দ্বারা সূচিত হবে। আবার OB∥AC হওয়ায় Q বলটি মানে ও দিকে AC দ্বারা সূচিত হবে।

অতএব P, Q ও R বল তিনটি মানে ও দিকে OAC ত্রিভুজের একই ক্রমে তিনটি বাহু যথাক্রমে OA, AC ও CO দ্বারা সূচিত হল।

বিকল্প প্রমাণ (ভেক্টর পদ্ধতি) (Alternative way of proof (vector method)):

মনে করি, O বিন্দুতে OX, OY, OZ বরাবর ক্রিয়ারত তিনটি বল P, Q ও R সাম্যাবস্থায় আছে।

OX ও OY থেকে কোনো নির্দিষ্ট এককের পরিমাপে যথাক্রমে OA এবং OB অংশ কটে নিই যেন উহারা P ও Q বলদ্বয়কে (মানে ও দিকে) সূচিত করে। OACB সামান্তরিকটি সম্পূর্ণ করে CO যোগ করি।

∴→=∴OA=P এবং →=OB=Q

আবার, $OB\Vert AC$ এবং =∴→=OB=AC∴AC=Q

এখন, +=→+→=→P+Q=OA+OB=OC   [সামান্তরিক সূত্রের সাহায্যে]

যেহেতু বল তিনটি সাম্যাবস্থায় রয়েছে

$\therefore P+Q+R=0$  বা, →+=0OC+R=0 বা, =−→=→R=−OC=CO

∴ P, Q এবং R বলত্রয়কে OAC ত্রিভুজের OA, AC ও CO বাহু দ্বারা মানে, দিকে ও একইক্রমে সূচিত করা যায়।

বলের লম্বত্রিভুজ সূত্র (Perpendicular triangle law of forces)

বর্ণনা (statement): কোনো বিন্দুতে ক্রিয়ারত তিনটি বলের মান যদি কোনো ত্রিভুজের একই ক্রমে গৃহীত তিনটি বাহুর সমানুপাতিক এবং দিক আনুষঙ্গিক বাহু সমূহের উপর লম্ব (সকল বলের দিক হয় বহির্মুখী অথবা অন্তর্মুখী) হয়, তবে বলগুলি ভারসাম্য সৃষ্টি করবে।

প্রয়োগ বিন্দুকে স্থির রেখে সবগুলি বলকে একই সাথে এক সমকোণে (90∘)(90∘) আবর্তন করলে, বল তিনটি একটি ত্রিভুজের একই ক্রমে গৃহীত বাহুত্রয় দ্বারা সূচিত হয়। সুতরাং বলের ত্রিভুজ সূত্রানুসারে বলগুলি সাম্যাবস্থা সৃষ্টি করে।

সাম্যাবস্থায় লামির উপপাদ্য (Lami’s Theorem of Equilibrium)

বর্ণনা (statement): কোনো বিন্দুতে ভিন্ন ভিন্ন রেখা বরাবর ক্রিয়ারত তিনটি সমতলীয় বল সাম্যাবস্থায় থাকলে, তাদের প্রত্যেকটি বলের মান অপর দুইটি বলের ক্রিয়ারেখার অন্তর্গত কোণের সাইনের সমানুপাতিক।

প্রমাণ: ভেক্টর পদ্ধতি (Proof: Vector method): মনে করি, O বিন্দুতে যথাক্রমে OX, OY ও OZ বরাবর ক্রিয়ারত P, Q ও R সমতলীয় বল তিনটি সাম্যাবস্থায় রয়েছে।

বলের সূত্র সম্পর্কে ধারণা নিয়ে বিস্তারিত :

আরও দেখুনঃ

• সিভিল কন্সট্রাকশন ১ – এসএসসি, ভোকেশনাল